Topology for Health Care Facilities’ Design
DOI:
https://doi.org/10.15168/xy.v2i3.48Abstract
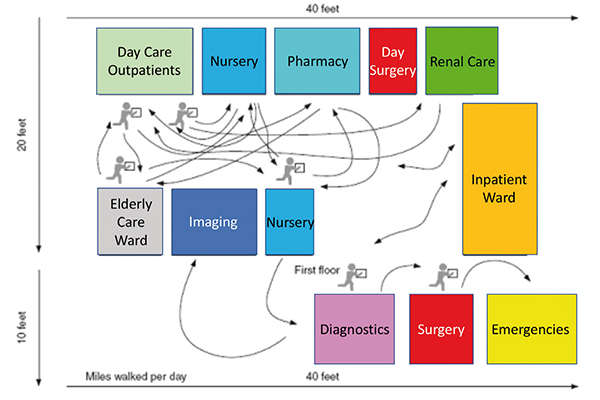
Mathematical concepts applied to painting, as well as to architectural design, arise frequently from intuition. The important role they play in design processes is being currently vindicated, as it is evidenced by artists and mathematicians as Lucio Saffaro. Topology is concerned with the properties of spaces that are preserved under continuous deformations, and has proved to be particularly useful in the previous stages of the architectural projects, when the location of uses and itineraries is defined. On the other hand, topology brings lots of possibilities in those phases of design where no dimensional definition is needed, but just to satisfy some spatial properties. It becomes then a powerful easy tool to show and analyse different solutions by means of their spatial relationships. Concepts as adjacency, connectedness, intersection, or inclusion, can be directly applied to layout schemes, setting the basis to further dimensioning. These concepts are traditionally managed and implemented by Geographic Information Systems (GIS), and are now being applied to architecture by means of Building Information Models (BIM). As a particular use, the architectural design of hospitals and other health care facilities benefits directly from topology’s properties. It is due, firstly, to their high complexity derived from their particular technical, functional, and equipment constraints. Secondly, topology becomes helpful to design the inner and outer itineraries of both people and logistics, paying attention to the specific problems derived from transfer points, pollution risks, and intersections. And thirdly, it permits to take into account the various possible users: patients, visitors, accompanying persons, staff, logistics suppliers, etc. The case study is a result of the research project (BIA2016‒78893‒C3‒1‒R) funded by the Spanish Ministry of Economy, Industry and Competitiveness, and the EU.
References
D’AMORE, B., 2014. Lucio Saffaro, le forme del pensiero. In D’AMORE, B. and SBARAGLI, S. (eds), Parliamo tanto e spesso di didattica della matematica. Atti del Convegno Nazionale Incontri con la Matematica, n. 28, Castel San Pietro Terme (Bo), 7‒9 novembre 2014. Bologna: Pitagora, pp. 193‒200.
DAUM, S. and BORRMANN, A., 2014. Processing of Topological BIM Queries using Boundary Representation Based Methods. Advanced Engineering Informatics. 28, 2014, pp. 272-286.
DAVIES, R. and HARTY, C., 2011. Building Information Modelling as Innovation Journey: BIM Experiences on a Major UK Healthcare Infrastructure Project. In HAUGBOLLE, K. et al. 6th Nordic Conference on Construction Economics and Organisation – Shaping the Construction/Society Nexus, vol. 2. Copenhagen, Denmark: Danish Society of Engineers Conference Centre, pp. 233‒246.
DEPARTMENT OF HEALTH UK, 2014. General design guidance for healthcare buildings. Available by: http://www.artsandhealth.ie/wp-content/uploads/2014/04/Health_building_note.pdf.
EGENHOFER, M.J., and HERRING, J., 1990. A mathematical framework for the definition of topological relationships. Proceedings of the 4th International Symposium on Spatial Data Handling. Zurich, Switzerland: International Geographical Union, pp. 803-813.
EVANS, J.R and MINIEKA, E., 1992. Optimization Algorithms for Networks and Graphs. New York: Marcel Dekker Inc., pp. 470.
HILLIER, B., 1996. Space is the Machine. Cambridge, Mass.: Cambridge University Press, pp. 368.
HILLIER, B. and HANSON, J., 1984. The Social Logic of Space. Cambridge, Mass.: Cambridge University Press, pp. 278.
KIM, H., JUN, Ch., CHO, Y., and KIM, G., 2008. Indoor Spatial Analysis using Space Syntax. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Vol. XXXVII, Part 2, 2008, pp. 1065‒1070.
LEE, J., 2001. A 3D data model for representing topological relationships between spatial entities in built-environments. PhD Dissertation. The Ohio State University. Available by: https://etd.ohiolink.edu/!etd.send_file?accession=osu1486399451960626&disposition=inline
LORENZ, B., OHLBACH, H.J. and STOFFEL, E., 2006. A hybrid spatial model for representing indoor environments. Web and Wireless Geographical Information Systems. 6th International Workshop, W2GIS 2006, Hong Kong, China, December 4-5, 2006. Berlin, Heidelberg, Springer Verlag, pp. 102-112.
PAUL, N., 2010. Basic Topological Notions and their Relation to BIM. In UNDERWOOD, J. and ISIKDAG, U. (eds) Handbook of Research on Building Information Modeling and Construction Informatics: Concepts and Technologies. Hershey, PA: IGI Global, pp. 451-472.
PENN, A., HILLIER, B., BANISTER, D., and XU, J., 1998. Configurational modelling of urban movement networks. Environment and Planning B‒Planning & Design. 25, 1, 1998, pp. 59‒84.
TANG, S.J., ZHU, Q., WANG, W.W., and ZFANG, Y.T., 2015. Automatic topology derivation from IFC building model for in-door intelligent navigation. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. XL-4/W5, 2015. 21-22 May, 2015. Tokyo, Japan. Available by: https://www.int-arch-photogramm-remote-sens-spatial-inf-sci.net/XL-4-W5/7/2015/isprsarchives-XL-4-W5-7-2015.pdf
VAN OOSTEROM, P.J.M., 1993. Reactive data structures for geographic information systems. New York: Oxford University Press, pp. 198.
WHYTE, J., 2002. Virtual Reality and the built environment. Oxford: Architectural Press, pp. 165.
YUAN, L. and ZIZHANG, H., 2008. 3D Indoor navigation: a Framework of Combining BIM with 3D GIS. In 44th International Society of City and Regiona Planners (ISOCARP) Congress, Dalian, China, September 19-23, 2008. Available at: http://www.isocarp.net/Data/case_studies/1187.pdf
ZLATANOVA, S., RAHMAN, A.A. and PILOUK, M., 2002. Trends in 3D GIS development. Journal in Geospatial Engineering, 4, 2, 2002, pp. 71-80.